3月15日

3月16日

1. 高次元力学系におけるホモクリニック軌道の精度保証法に向けて / ○新田 光輝 (電気通信大学), 山本 野人 (電気通信大学) [概要]

   精度保証付き数値計算を応用することで力学系の解析を行うことが近年盛んに行われており、連続力学系におけるホモクリニック軌道やヘテロクリニック軌道の精度保証などはその典型である。しかし、既存の方法は三次元までの問題に限定された方法である場合がほとんどである。そこで、本講演では、より高次元の系のホモクリック軌道の存在検証に利用できる精度保証法について、特に不安定多様体の精度保証による捕捉に焦点を絞り説明を行う。

2. 連続力学系の非双曲型平衡点近傍での疑似Lyapunov関数の構成と精度保証 / ○寺坂 元 (電気通信大学　情報・ネットワーク工学専攻), 中村 正男 (電気通信大学　情報・通信工学専攻), 山本 野人 (電気通信大学　情報理工学研究科) [概要]

   連続力学系の双曲型平衡点の近傍では二次形式によるLyapunov関数が構成可能であり、精度保証に依る構成法もいくつか知られている。これに対し、非双曲型平衡点の近傍では、二次形式のLyapunov関数は原理的に構成することができない。本講演では、３次元以上の系において解軌道を位相空間内の超平面に射影した軌道を考え、非双曲な平衡点のこの超平面における像の近傍でのLyapunov関数を二次形式で構成することを試みる。あわせて、その精度保証に依る構成法を導出し、数値例で有効性を確認する。

3. 微分方程式の初期値問題に対するDE-Sinc-Nyström法の改善 / ○原 涼太 (広島市立大学), 岡山 友昭 (広島市立大学) [概要]

   本研究では，微分方程式の初期値問題に対する数値計算法を考える．その１つとして，NurmuhammadらがDE-Sinc-Nyström法という方法を提案している．これはDE変換とSinc不定積分法に基づく方法であり，特に数値実験結果より，stiffな問題にも頑健な方法であると報告されている．ただし，そこで用いられているDE変換には逆関数が初等関数では表せず，改善の余地がある．本研究では逆関数が初頭関数で表せるDE変換を用いたDE-Sinc-Nyström法を提案する．

4. 佐藤超函数論に基づくフーリエ変換の数値計算法 / ○緒方 秀教 (電気通信大学大学院情報理工学系研究科情報・ネットワーク工学専攻) [概要]

   佐藤超函数論は複素関数論に基づく一般化関数論であり、そこでは「超函数」は解析関数F(z)（これを超函数の「定義関数」と呼ぶ）の境界値の差F(x+i0)-F(x-i0)で表される。本講演ではこの佐藤超函数論に基づいたフーリエ変換の数値計算法を提案する。フーリエ変換も佐藤超関数論においては複素解析関数の境界値の差で表され、その解析関数すなわち定義関数はフーリエ変換を計算しようとする関数を含む半無限区間積分で与えられる。本方法ではまずこの定義関数を数値積分により、複素平面内の点における冪級数の形で求める。そして、この冪級数を連分数展開の形に変換して実軸の近くへ解析接続し、境界値の差としてフーリエ変換を求める。この方法によれば、計算の難しい無限区間上の振動積分の計算を避けることができ、フーリエ変換を高い精度で計算することができる。講演では本方法の詳細について説明し、数値実験例により本方法の有効性を示す。

1. 離散エネルギー最小化による重み付き多項式補間の構成 / ○平野 広明 (東京大学 大学院情報理工学系研究科 数理情報学専攻), 田中 健一郎 (東京大学 大学院情報理工学系研究科 数理情報学専攻) [概要]

   減衰の度合いを利用し補間を行う手法に重み付き多項式補間がある．高精度な標本点の選ぶためには，誤差の上からの評価値を最小化する問題を解けばよいと考えられる．本研究ではポテンシャル論からの類推を利用し，近似問題として離散エネルギー最小化問題を解いて標本点を得た．離散エネルギーを用いた誤差評価について述べ，数値実験結果を示して高精度な公式が構成できていることを確認する．

2. modified Hunter–Saxton方程式に対する差分法の安定性と収束性 / ○佐藤 峻 (東京大学) [概要]

   表面張力波の発展を記述するmodified Hunter-Saxton方程式の初期値問題は，混合微分を含むために取扱いが難しい．最近になって時間局所適切性が示されたが，解の挙動は十分に解明されておらず，信頼できる数値解法が必要である．本研究では，不変量を上手く利用して安定性と収束性をもつ数値解法を構築する．講演では，数値解法の解析における混合微分特有の困難とその解決策を主に紹介する．

3. 散逸型微分方程式に対する各種モデル縮減手法の検討 / ○柳澤 広大 (東京大学), 松尾 宇泰 (東京大学) [概要]

   モデル縮減とは，高次元微分方程式系の数値計算高速化を目的として，現象を近似する低次元系を構築する手法の総称である．一般には固有直交分解で部分空間を一つ構築し，それを用いてGalerkin projectionによって低次元系を構築するが，近年ではその拡張としてCarlbergら（2011）のPetrov-Galerkin projectionやAmsallemら（2012）の複数部分空間構築手法が盛んに研究されている．本発表では散逸型微分方程式を対象にこれらの性能評価を行った結果を報告する．

4. 南部括弧に基づく構造保存数値解法に関する一考察 / 杉渕 優也 (東京大学), ○松尾 宇泰 (東京大学), 佐藤 峻 (東京大学) [概要]

   ある種の偏微分方程式は，Poisson，あるいは南部括弧を用いて表現でき，その帰結として自然にHamiltonianなどの保存性が示される．これらの括弧表現は数値計算にも有用であり，例えばSalmon(2005)では，浅水方程式に対する南部括弧表現の巧妙な空間離散化で，複数保存量を持つ，いわゆるArakawa-Lamb半離散スキームが得られることを指摘している．本発表ではこれに時間方向の構造保存離散化が組み合わせられ，帰結として複数保存全離散スキームが得られることを報告する．

1. Linear Systems in Matlab with Zero Residual / ○Rump Siegfried M (Hamburg University of Technology) [概要]

   Several examples of linear systems are given for which the residual of the computed approximation is precisely zero, Matlab's backslash operator is highly inaccurate, and no warning is issued.

2. Improved results for accurate summation / ○Lange Marko (早稲田大学) [概要]

   Many algorithms for accurate summation are based on error-free transformations of sums. A particularly important result is Dekker’s theorem for the FastTwoSum function. In this talk, we introduce a new result leading to weaker conditions than the ones proved by Dekker. Together with other new results, we prove that our summation algorithm computes the same accurate sums as Zhu and Hayes’s OnlineExactSum or Rump’s FastAccSum algorithm while performing better.

3. 行列積の下向き丸めと事前誤差評価を用いた連立一次方程式の精度保証付き数値計算法向けの高精度な誤差評価式の提案 / ○南畑 淳史 (AIST), 荻田 武史 (東京女子大学), 大石 進一 (早稲田大学) [概要]

   IEEE754の丸めモードを用いた上向き丸めの計算結果と下向き丸めの計算結果を利用した行列積の包含は非常に精度が良く、連立一次方程式の精度保証付き数値計算において広く使用される。 本発表では下向き丸めの計算結果と事前誤差評価を利用した高速な行列積の包含を利用した連立一次方程式の精度保証付き数値計算に適した近似解と真の解の誤差評価式を提案する。

4. 区間行列に対する正則性の高速な保証法 / ○寺尾 剛史 (芝浦工業大学), 尾崎 克久 (芝浦工業大学) [概要]

   与えられた行列が正則であることを保証する計算機援用証明法は多く提案されている．これらの手法の多くは入力として点行列を扱うものが多かったが，我々は点行列に対する高速精度保証法を区間行列に対して拡張を行った．本発表では，各手法における数値実験の結果とその解析結果を紹介する．

1. 行列積に対する隣接浮動小数点丸めの結果を返すアルゴリズム / ○尾崎 克久 (芝浦工業大学) [概要]

   成分が浮動小数点数である行列の積を高精度に計算する．エラーフリー変換を部分的に用い，精度については隣接浮動小数点丸め（faithful rounding）を達成する高速な計算手法を提案できた．問題が両条件である場合，近似計算の約6倍程度の計算時間で隣接浮動小数点丸めを達成できること数値実験により確かめた．

2. 浮動小数点フィルタの応用と性能評価 / ○太田 悠暉 (芝浦工業大学大学院), 尾崎 克久 (芝浦工業大学) [概要]

   数値計算の結果の符号を保証する浮動小数点フィルタは多く提案されてきた． 我々は絶対誤差の上限が与えられたときに，浮動小数点フィルタを自動的に作成する方法を開発してきた． 本発表ではその性能に関する考察を与え，浮動小数点フィルタを絶対誤差や相対誤差の保証に用いる試みについて紹介する．

3. 高精度な内積計算の分散並列用アルゴリズムとその応用 / ○落合 涼太 (芝浦工業大学大学院), 尾崎 克久 (芝浦工業大学) [概要]

   本発表では、拡張した高精度内積計算アルゴリズムと、その分散並列アルゴリズムおよびその誤差評価の紹介を行う。本アルゴリズムはBLASに存在する行列・ベクトル積関数と同様の計算を疑似四倍精度で計算でき、その誤差上限も出力できる。最後に超大規模計算環境における本アルゴリズムの現状と応用例について紹介する。

4. 丸め誤差を利用した計算順序を特定する例題について / ○坂本 篤志 (芝浦工業大学大学院), 尾崎 克久 (芝浦工業大学) [概要]

   浮動小数点数を扱う数値計算において丸め誤差解析を行う研究がある．問題の計算順序が決まっていれば，任意の計算順序に対する丸め誤差評価式よりも良い式を利用することができるが，ソースが公開されてない, またはコードの解読が困難などの理由から計算順序がわからない場合がある. そこで本発表では，いくつかの仮定のもと，計算結果から内積計算の計算順序を特定するための例題を紹介する．

1. 高速で拡大する自己相似な面外亀裂の特異積分方程式 / ○平野 史朗 (立命館大学理工学部), 伊藤 弘道 (東京理科大学理学部) [概要]

   地震時の断層破壊には, 1) せん断波速度の40-90%程度の高速破壊, および 2) 弾性波として放射されるエネルギーの総和が破壊継続時間の3乗に比例, という特徴がある. 前者は動弾性によるモデル化の必要性を, 後者は系の自己相似性を示唆している. つまり動的問題であっても空間変数と時間変数の比だけで系が記述できる. 地震学で広く用いられる積分方程式がそれによってどのように記述できるかを考察する.

2. 大規模非線形粘弾性有限要素法による沈み込み帯での地震後地殻変動計算 / ○縣 亮一郎 (海洋研究開発機構), Barbot Sylvain (南洋理工大学), 藤田 航平 (東京大学), 兵藤 守 (海洋研究開発機構), 中田 令子 (海洋研究開発機構), 飯沼 卓史 (海洋研究開発機構), 市村 強 (東京大学), 堀 高峰 (海洋研究開発機構) [概要]

   2つのプレートが衝突する沈み込み帯での巨大地震発生後には，マントルでの粘弾性緩和と地震発生領域周囲での地震後断層すべりが原因と考えられる地震後地殻変動が生じる．本研究では，前者を岩石実験由来の非線形構成則，後者を断層面上の摩擦則によりモデル化した，沈み込み帯の複雑三次元構造における大規模有限要素計算により，少ないパラメータチューニングで東北地方太平洋沖地震後の地殻変動をよく説明することに成功した．

3. 箱根火山で観測された地震動と空振の関係について-差分法を用いた考察- / ○若松 修平 (立命館大学), 平野 史朗 (立命館大学), 川方 裕則 (立命館大学) [概要]

   箱根火山では、2015年4月下旬から火山活動が活発化し、7月1日に噴火に伴う空振(低周波の音波)も観測された。この空振によるシグナルは空振計だけでなく、地表に設置された地震計にも記録されていた。この地震計のシグナルの強さは、火口から観測点までの距離に反比例していなかった。本研究では、箱根火山で発生した空振の伝播について差分法を用いたシミュレーションを行うことで、空振の伝播について地形が与える影響について考察した。

4. ３次元移流問題のためのアダプティブ Lagrange-Galerkin スキーム / ○二井 滉太 (金沢大学), 野津 裕史 (金沢大学) [概要]

   局所的にメッシュを細かくするアダプティブメッシュリファインメントと流れ問題の強力な数値解法の一つであるLagrange-Galerkin(LG)法を組み合わせたアダプティブLG法を提案する。アダプティブLG法を3次元移流問題に対して実装した数値計算結果を誤差や計算時間等の観点から調べて報告する。

1. Poisson方程式に対する粒子法の離散H^1_0ノルムによる安定性 / ○井元 佑介 (東北大学　知の創出センター) [概要]

   Navier-Stokes方程式に対する多段解法で現れる圧力Poisson方程式のような，右辺項が既知関数の発散で表されるPoisson方程式に対して，粒子法の近似微分作用素を用いて離散化したPoisson方程式を考える．本講演では，このPoisson方程式に対する粒子法の最大値ノルムによる誤差評価を示し，さらに，発散の近似微分作用素を適切に選択し，粒子法における離散H^1_0ノルムを導入することで，従来の結果より緩い条件の下で安定性が得られることを示す．

2. 不連続ODE系で記述される閉じ込められた粒子運動の一意可解性 / ○楊 振興 (金沢大学), 木村 正人 (金沢大学), van Meurs Patrick (金沢大学) [概要]

   現在、粒子法と呼ばれる数値計算方法がある。有限要素法との差異は、計算格子を作る必要がない代わりに連続体がたくさんの粒子で構成されていると考え、その粒子たちの動きを計算する点にある。今、ある領域に閉じ込められた粒子を考え、粒子が境界に接触するとき、粒子の速度ベクトルが変化すると仮定する。この問題は不連続常微分方程式系である。この問題の解の存在性と一意性を説明する。

3. 振動剥離現象のモデリングとその有限要素解析 / ○米田 拓朗 (金沢大学), 木村 正人 (金沢大学), Scala Riccardo (Faculdade de Ciências da Universidade de Lisboa) [概要]

   本研究では，ある2つの弾性体が接着剤で接着しているときに振動を加え，接着力が弱まり，最終的に剥離するまでの現象の数理モデルのシミュレーションとその解析を行った．今回用いる剥離モデルはR.Scala氏(ESAIM:COCV,2017)の論文で用いられた弾性波動方程式である．本研究では，「剥離モデルの有限要素法」，「接合領域問題の可解性」，「領域反復法による数値シミュレーション」の3点について調べた．本研究は木村正人氏(金沢大学), R.Scala氏(Faculdade de Ciências da Universidade de Lisboa)との共同研究である．

4. 2次元波動方程式の時間域境界積分法の安定性に関する一考察 / 福原 美桜 (京都大学), 三澤 亮太 (京都大学), 新納 和樹 (京都大学), ○西村 直志 (京都大学) [概要]

   2次元波動方程式の時間域境界積分法の安定性の問題は，ある非線形固有値問題に帰着されることを示す．この固有値問題を櫻井・杉浦法で数値的に解き，時間域境界積分方程式法を用いた数値実験結果と合致することを示す．

1. 懸濁液の数学解析〜先端付近で生じる隆起現象〜 / 松江 要 (九州大学マス・フォア・インダストリ研究所/カーボンニュートラル・エネルギー国際研究所), ○友枝 恭子 (摂南大学理工学部基礎理工学機構) [概要]

   傾斜角を持つアクリル製の斜面に分散が均一のガラズビーズ（粒子）とシリコンオイルの懸濁液を流す. このとき, 傾斜角が高くかつ粒子の体積分率も高いと 流下する懸濁液の先端には粒子が集まり, 懸濁液の縁部分が粒子塊によって隆起する. これはZhou等(2005)の実験結果の一部である. 彼らの結果によると, この隆起現象は2つの衝撃波(1-衝撃波と2-衝撃波)によるものとされているが, 提唱された数理モデルに対する弱解のパターンを調べると, 必ずしも隆起現象は2つの衝撃波によるものではない可能性が生じた. 本講演では, これらの弱解の構成パターンを紹介し, 隆起現象と衝撃波の関係を探る.

2. Mathematical analysis of molecular communication network model / ○本多 泰理 (NTTネットワーク基盤技術研究所) [概要]

   近年提案されている、分子通信に基づくdrug deliveryのための数理モデルを対象として、空間２次元の場合におけるモデルの記述と数学解析を行う。

3. 固有値問題における一般J積分 / ○大塚 厚二 (広島国際学院大学) [概要]

   偏微分方程式の境界値問題における固有値をコスト関数とする形状感度を一般J積分で表現する。ここでの一般J積分は固有関数が強解になったとき、ゼロとなる性質を持つ積分形式のことで、従来の一般J積分とは少し異なる。一般J積分の利点は、形状感度の領域積分表示から境界積分表示への変換が自動的に可能で、混合境界問題での特異性にも対応できる点にある。

4. 半導体 drift-diffusion 方程式の混合型有限要素法と線形ソルバー / ○鈴木 厚 (大阪大学 サイバーメディアセンター) [概要]

   Drift-diffusion 方程式は半導体デバイスの数理モデルである. 電子と正孔密度分布は静電場への指数関数依存性を考慮した有限体積法である Scharfetter-Gummel スキームにより離散化を行なうことが多いが, その勾配である電子/正孔電流を離散化する混合型有限要素近似を用いることを考える. 指数関数依存性は静電場の要素毎の区分一次近似により自然に扱うことができる. 離散化により不定値の係数行列が得られるが, 適切な対角スケーリングと対称軸選択を用いる直接法により LDU 分解でき, 解を得ることができる.

1. 対称2枚貼り折紙法のサイドメンバーへの適用性評価 / ○中野 秀太 (京都大学), 杉山 文子 (京都大学) [概要]

   対称2枚貼り折紙法を用いたサイドメンバーを作ることを想定し、衝撃特性、振動特性などを数値解析で調べた。

2. 折り畳み構造を利用した防振機構の荷重範囲の拡張と周波数特性 / ○稲本 知也 (明治大学理工学部機械工学科), 石田 祥子 (明治大学理工学部機械工学科) [概要]

   Kresling patternからなる円筒型折り畳み構造は双安定性を有し，この構造に線形ばねを付加した防振機構が開発されている。本研究では，本防振機構の設計変数の変更や線形ばねの付加位置の検討を行った結果，従来の防振可能な荷重範囲を3倍以上拡張することができた。さらに，拡張された荷重範囲における本防振機構の防振性能を加振実験によって検証した。本講演では，荷重範囲の拡張を可能にした防振原理および本防振機構の周波数特性について報告する。

3. 組立式トラスコアパネル（ATCP）の実用化に向けた立体コア折紙構造の検討 / 萩原 一郎 (明治大学), 寺田 耕輔 (福島高専), ○阿部 綾 (明治大学) [概要]

   オクテット型トラスコアは野島武敏らにより考案された四面体と八面体から成る空間充填で構築された構造である。寺田耕輔らはそれらのアスペクト比の限界を克服する折り畳み方法を提案し、その結果、展開図に基づき、切断および曲げ工程の後、コアをATCP（アセンブリトラスコアパネル）と呼ばれるパネル形状に組み立てることが可能となった。 ここでは、ATCPの有利な特性について検討し、今後の展望について言及する。

4. 環状折り畳み構造の展開図作成法と剛性検証 / ○海野 真誼 (明治大学理工学部機械工学科), 石田 祥子 (明治大学理工学部機械工学科) [概要]

   これまでに，高い剛性を持ちかつ端部の駆動だけで展開が可能という二つの特徴を持つ折り畳み構造が米国アカデミー紀要に報告された。本研究では，この構造の開口部にフタとなる部品を必要とせず，展開時の形状に多様性を持たせることを目的に，この折り畳み構造を環状へと変換した。本講演では，Matlabによる環状折り畳み構造の展開図作成法と，容易に展開可能か検証した結果を報告する。また，モード解析による本構造の剛性についても述べる。

5. 正四面体／八面体の折り畳み式厚板ボックスとシミュレーション / ○奈良 知惠 (明治大学 MIMS), 阿部 綾 (明治大学 MIMS), 平田 浩一 (愛媛大学 教育学部), 萩原 一郎 (明治大学 MIMS) [概要]

   折畳み式製品の開発は重要であり，素材によって多様な課題が生じるため，離散幾何学と折紙工学を融合することによって解決の糸口が得られると期待される。本講演では，すでに解決済みの直方体の折り畳み式厚板ボックスに続き研究を進めている，正四面体と正八面体の折畳み式厚板ボックスについて得られた結果を紹介する。

1. 正四面体から凸多角形への展開について / 西村 憲明 (龍谷大学), 上薗 拓郎 (龍谷大学), ○山岸 義和 (龍谷大学) [概要]

   正四面体を展開して得られる凸多角形が三角形、四角形、五角形、六角形に限ることは Akiyama et al. (2006) によって示された。Akiyama-Nara (2007) は、斜交座標の格子点との関係によって、これらの凸多角形を網羅した。本講演では、正四面体を一本の輪に切り開く展開と、Akiyama-Nara の定理を利用して、切り込みのグラフの形によって凸多角形の作り方が簡潔に分類できることを示す。

2. 双対タイリング折り紙 / ○安達 瑛翔 (東京大学), 舘 知宏 (東京大学), 山口 泰 (東京大学) [概要]

   Lang の作品 Octet Truss を一般化して双対タイリング折り紙を定義、必要十分条件を確認する。この折り紙は双対関係に対応するトラス構造を持ち表面ライナーと全面で接着する板材になる。任意の平行四辺形格子に対し平面間の距離を十分とるならば双対タイリング折り紙が存在する。また二つの円筒ねじれ折りパターンの間を充填する折り紙について議論する。

3. 三次元形状を折りたたみ可能な立体に自動変換する手法の提案 / ○宮本 惠未 (筑波大学), 遠藤 結城 (筑波大学), 金森 由博 (筑波大学), 三谷 純 (筑波大学) [概要]

   ものを平坦に折りたたむことは空間を要領よく使う上で有効な手段だが、その設計には試行錯誤が必要であり、任意形状の再現は難しい。先行研究によって，より自由度の高い形状を持つ折りたたみ可能な立体の設計システムが提案されたが、操作が直感的でないという問題がある．そこで本研究では入力された三次元形状を折りたたみ可能な立体へと自動的に変換する手法を提案する．本手法によって先行研究よりも少ない作業コストで目的を達成できた。

4. 正四面体の cut locus / ○物部 侑吾 (龍谷大学), 山岸 義和 (龍谷大学) [概要]

   正四面体の測地的距離による cut locus は、平面のボロノイ分割として表される。合同な四枚の二等辺三角形からなる四面体で、展開図が平面の周期的タイル張りを与えるものに対する cut locus についても、その分岐図について報告する。

1. ドライバー理解に向けたドライバーモニタリング技術の進化 / ○木下 航一 (オムロン株式会社) [概要]

   近年、運転中のドライバー状態を測定するためのドライバーモニタリング技術への関心が急速に高まっている。本講演ではこの社会的背景について解説した後、時系列ディープラーニングを活用した高精度なドライバー状態推定技術、さらにより深い内面状態推定に向けた最新の開発事例等を紹介する。

2. 行列分解型ディープニューラルネットワーク計算法および単一細胞解析への応用 / ○今倉 暁 (筑波大学), 荒井 亮祐 (筑波大学), 櫻井 鉄也 (筑波大学, JST/CREST), 野村 暢彦 (筑波大学, JST/ERATO), 八幡 穣 (筑波大学, JST/ERATO) [概要]

   画像認識や音声解析などの分野においてディープニューラルネットワーク（DNN）計算が成果を上げており活発に研究が進められている。本講演では、標準的手法であるバックプロパゲーション（BP）法と異なるアプローチに基づくDNN計算法として、近年我々が開発を進める行列分解型DNN計算法およびその改良法について示す。また、その応用事例として単一細胞解析への適用事例についても併せて紹介する。

1. LUBAC依存的なNF-κB活性化メカニズムの数理的解明 / ○濱田 大輔 (大阪大学大学院基礎工学研究科システム創成専攻数理科学領域) [概要]

   リンパ球の一種であるT細胞では，受容体が刺激を受けることによりNF-κBが活性化される．このシグナル伝達経路において，LUBACと呼ばれるユビキチンリカーゼが影響していることが分かった．LUBACはCBM複合体に直鎖状ユビキチン鎖を付与し，IKK複合体のリン酸化に影響を与え，その結果NF-κBの活性化につながる．本研究ではこの反応におけるLUBACの役割について理解するため，数理モデルを作成した．その数理モデルをシミュレーションによって数学的に解析した結果を発表する．

2. Single Multiciliated Cell Apical Cytoskeleton Active Hydrodynamic Simulation with FreeFEM++ / ○Franco Fermin (阪大院医) [概要]

   The apical cytoskeleton of Multiciliated Cells (MCC) tend to align in a series of stripes, passing through several stages. Basal bodies (BB) of MCCs tend follow the alignment of the cytoskeleton. The BBs tend to orient their basal feet (BF) towards the cytoskeleton at an angle. In order to model the alignment and orientation of BBs we first model the alignment stages of the cytoskeleton. Real cells have a changing irregular shape, approximately hexagonal but, so far, simulations do not account for the cell shape, difficult to handle by the method of Finite Differences. On the other hand, the Finite Element Method is suitable to handle different shapes and fine emerging structures in the solutions. We propose the FreeFEM++ language for simulating the the Active Hydrodynamics Equations of the cytoskeleton. The alignment stages of the cytoskeleton are reproduced with good agreement of the timescales. The Finite Element Method allows for precise solutions and flexibility on the cell boundary shape.

3. 医療保険におけるレセプトの基本統計分析のピリオド法を用いた改善について / ○村山 令二 (健康保険組合連合会) [概要]

   医療保険の保険者は、加入者全体の受診の基本統計を、受診した医療機関のレセプトに関する特定項目のみの集計表から作成する。 患者の受診状況を微分方程式で表し、ピリオド法の考え方を用いると、これまで、レセプトの集計表からは得られず、医療機関対象の患者調査からのみ得られるとされていた入院の平均在院日数・在院患者数や外来の平均通院間隔・通院患者数などの基本統計を、レセプトの集計表から推定する公式が得られる。

1. レーザーカオスを用いたTHz波による分光 / ○桑島 史欣 (福井工大), 白尾 拓也 (福井工大), 岩尾 憲幸 (福井工大), 合田 汐⾥ (福井工大), ⾕ 正彦 (福井大遠赤セ), 栗原 一嘉 (福井大教育), 山本 晃司 (福井大遠赤セ), 森川 治 (海保大), 北原 英明 (福井大遠赤セ), 中嶋 誠 (阪大レーザー研) [概要]

   レーザーカオスにより発生した高安定なテラヘルツ波は、帯域は0.1～1THzの範囲であり、特に0.3THzは水の吸収の少ないオープンすぺすでの通信に最適な最高周波数帯である。 この電磁波の発生方法および分光への応用について講演する。

2. 多モード半導体レーザーにおけるモード成分間の同時発振性 / ○和田 健司 (大阪府立大学工学研究科), 松山 哲也 (大阪府立大学工学研究科) [概要]

   テラヘルツ時間領域分光法（THz-TDS）に利用されている戻り光多モード半導体レーザーからのカオス光に対して，モード成分間の同時発振性を調べることを目的とし，その前段階として，ランジュバンノイズによって揺らいだ多モード半導体レーザー出力を対象に，モード成分間の同時発振性の程度をTHz-TDS出力をシミュレートすることにより見積もる．

1. パーセバルの等式を考慮したDFT検定における参照分布の定量的・理論的考察 / ○岩崎 淳 (福岡工業大学) [概要]

   NIST 乱数検定ツールに含まれるDFT検定は，乱数列に離散フーリエ変換を施し、得られたフーリエ系数を基に検定を行う乱数検定法である．最初期のものは周波数ごとのフーリエ系数の分布が互いに独立であると仮定して参照分布が導出されていたが，参照分布の分散が実験的な評価と整合せず、実験的・数値的に補正された参照分布が現在は用いられている．一方、フーリエ系数の分布が互いに独立とみなせない理由について，山本らはパーセバルの等式による制約であると主張し、参照分布の分散が整合しないことを定性的に説明した．本発表では，パーセバルの等式による制約を考慮して，一定のモデルを仮定したうえで，参照分布の分散を定量的・理論的に評価する．また，数値的な評価を行い，仮定されるモデルの妥当性について議論する．

2. NIST SP.800-22に含まれるDFT検定に関する考察 / ○奥富 秀俊 (東芝情報システム) [概要]

   NIST SP.800-22（以下NIST乱数検定と呼ぶ）は今日最も広く使われている統計的な乱数検定セットである． NIST乱数検定に含まれるDFT検定は，多くの研究者により誤りが指摘され，同時に修正案が提示されている． 本発表では，本DFT検定を構成するステップのどこに誤りが混在したかについて整理しながら，一方で，根本原理に基づく初歩的な検定法の一案について触れる．

3. 乱数性の劣る2値系列を用いた乱数検定の特徴付けについて / ○山口 明宏 (福岡工業大学), 斉藤 朝輝 (公立はこだて未来大学) [概要]

   一般に乱数検定は複数の異なる種類の乱数検定の集合として定義されるが，個々の乱数検定の間の独立性は自明ではない．本研究では，僅かに乱数性が劣る2値系列を用意し，その乱数性の判定結果をもとに乱数検定の特徴付けを行った結果を報告する．更に乱数検定のミニマルセットとの関連についても議論する．

1. 二次元光双安定素子を用いたナチュラルコンピューティング：波面伝播制御と外部フィードバックによる高機能化 / ○礒島 隆史 (理化学研究所) [概要]

   2次元的広がりを持つ光双安定素子では、2つの安定状態領域間の遷移面が波面として伝播する。我々は、これを用いて迷路探索をはじめとする情報処理のためのナチュラルコンピューティング素子の実現を目指している。本発表では、温度により光透過率の変化する液晶を用いた熱型光双安定素子について、三次元有限要素法シミュレーションで素子動作条件の検討を行うとともに、外部フィードバックによる動作モードの高機能化の試みを紹介する。

2. 広帯域ランダム光注入を受けるカスケード結合レーザのPrincipal Frequency Band / ○奥田 勇気 (鳥取大学), 吉村 和之 (鳥取大学) [概要]

   カスケード結合半導体レーザ系の広帯域ランダム光注入に対する応答を数値的に調べた。Consistencyと呼ばれる性質を有する場合、レーザ系の出力光波形は、注入光波形により完全に定まる。このとき、出力光波形に強く影響を与える注入光の周波数帯を、Principal Frequency Band (PFB)と呼ぶ。本講演では、カスケード結合半導体レーザ系について、PFBの各種パラメータ依存性を調べた結果を報告する。

3. カオス尺度による気液二相流シミュレーションデータの取り扱い / ○井上 啓 (山陽小野田市立山口東京理科大学), 平野 博之 (岡山理科大学) [概要]

   淡水魚と海水魚を同じ水槽内で飼育するために適した水槽の形状を検討する研究が行われている。同研究では、実際の水槽を用いた実験だけでなく、実験結果を再現する数値流体シミュレーションも同時に行われている。本発表では、同検討に用いられている気液二相流モデルの数値シミュレーションデータをカオス尺度を用いて評価することを試みる。

4. カオス尺度の性質に関する調査 / ○真尾 朋行 (東芝情報システム株式会社), 奥富 秀俊 (東芝情報システム株式会社) [概要]

   生体データ（主に心拍間隔データ:RRI）の分析において，カオス性の指標としてカオス尺度を用いることを検討している． 本発表では，カオス尺度の性質について調査した内容を報告する．

1. 戸田の双対変換とルジャンドル変換の関係 / ○後藤 振一郎 (京都大学), 和田 達明 (茨城大学) [概要]

   １９６７年に戸田格子が発表されたが、その発見の基礎になったのが、双対変換と呼ばれる座標変換である。格子ハミルトン系にこの変換が適用される場合、系は双対格子と呼ばれ、具体例として線形格子と戸田格子等が知られている。本講演ではこの双対変換がある意味でルジャンドル変換と深く結びついていることを示し、この事実を用いることにより、双対格子を無限個構成できることを示す。

2. Fermi-Pasta-Ulam格子における対称Discrete Breather解の存在と安定性 / ○吉村 和之 (鳥取大学) [概要]

   Discrete Breather (DB)は，空間的離散性と非線形性を備えた力学系における空間的に局在した周期解である。本講演では、 Fermi-Pasta-Ulam 格子モデルに関して、Sievers-Takeno mode、および、Page mode と呼ばれる２種類の異なる空間対称性を有するDB解の存在証明とスペクトル安定性に関する結果を示す。

3. 非対称相互作用をもつ結合カオス系の拡散共鳴(Spreader Resonance)について / ○梅野 健 (京都大学大学院情報学研究科) [概要]

   コーシー分布の加法性を基礎に、コーシー分布を不変測度とする一方向結合系で、厳密な条件付きリヤプノフ指数が計算でき、 カオス同期が起こるか否かの判定(閾値)が厳密に行えることが解っている[1]。2017年の年会では、それを場の理論に一般化した結果 を報告したが、本報告では、双方向で非一様に結合した系(自由度が２の系)で、２つの力学変数の不変測度(極限分布)を与える コーシー分布の尺度母数が、有限の結合定数で無限大に発散する”拡散共鳴(Spreader Resonance)”と言う新しい 現象が起きていることを報告する。 [参考文献] [1]M. Shintani and K. Umeno, “Conditional Lyapunov exponent criteria in terms of ergodic theory”, Prog. Theor. Exp. Phys. (2018), 013A01 (15 pages) DOI: 10.1093/ptep/ptx168

1. 格子凸多面体とその双対におけるエルハルト多項式の根の分布 / ○山田 祐見 (筑波大学システム情報工学) [概要]

   エルハルト多項式は格子凸多面体の含む格子点を数え上げる面白い多項式であり，その根の分布について多くの関心を集めている．本講演では，3次元reflexive polytopeという格子凸多面体のエルハルト多項式の根の分布に関する計算機を用いた計算による分類結果を示す．さらに，2，3次元reflexive polytopeとその双対との根の分布に関する計算の結果を示し，以上の結果から高次元一般に関する予想を示す．

2. 有理凸多面体に含まれる整数点の数え上げ問題に対する数値積分からのアプローチ / ○大城 隆之介 (東京大学), 平井 広志 (東京大学) [概要]

   有理凸多面体に含まれる整数点の数え上げ問題に対する手法の１つとして Lasserre and Zeron (2003) によるZ変換を行なった後に逆Z変換を計算するというものがある。 本講演ではまずこの逆Z変換を数値積分を用いて行うことを考えたときの誤差評価を行う。その後、数値積分の誤差評価から導き出される集合の分割の数え上げやグラフの完全マッチングの数え上げに対するアルゴリズムについて述べる。

3. k-交換システムに対する巨大近傍を用いた局所探索法 / ○江藤 巧馬 (九州大学), 神山 直之 (九州大学) [概要]

   本発表では，k-交換システムにおける最大独立集合問題を考える．この問題に対しては Feldman et al. (2011) によって多項式時間(k/2 + \epsilon)-近似アルゴリズムが存在することが示されている．本発表では，この問題に対して準多項式時間 ((k+1)/3 + \epsilon)-近似アルゴリズムを提案する．このアルゴリズムはCygan et al. (2013) が提案したk-ハイパーグラフマッチング問題に対する準多項式時間((k+1)/3 + \epsilon)-近似アルゴリズムの拡張となっている．

4. Polymatroid-based capacitated packing of branchings / ○松岡 達也 (東京大学), Szigeti Zoltán (Université Grenoble Alpes, Grenoble INP, CNRS, G-SCOP) [概要]

   Durand de Gevigney, Nguyen and Szigeti (2013) generalized spanning arborescence packing problem by using a matroid and solved that problem. We consider two polymatroid-based capacitated packing problems, which are the generalization of this problem. We give the condition for the existence of a feasible solution and a strongly polynomial-time algorithm for one problem. For the other problem, we show strong NP-completeness.

1. A Method for Discovering the Knowledge of Item Rank from Consumer Reviews / ○羅 松 (筑波大学大学院　システム情報工学研究科) [概要]

   When observing a collection of items ranked in a linear order, we may be interested in the questions that why and how one item is ranked over another. When consumer reviews of the ranked items are also observed, this paper presents a method for discovering the knowledge of the rank of the items from the consumer reviews. The basic idea of the method is to construct a choice model and then to build it in the learning theory. This idea formulates the questions of interest as a biconvex optimization problem which has a relationship with SVM (Support Vector Machine). To facilitate the process of knowledge discovery, we develop a two-stage learning algorithm. In the first stage, we extract as much information as possible from the observed data, while in the second stage, the extracted information is further summarized into knowledge. Finally, we evaluate the method by showing our simulation result of the learning algorithm and experimental result of a real-world problem.

2. ネットワーク最適化における LP 拡張定式化を与える通信プロトコルの構成 / ○牛丸 陽太 (東京大学大学院情報理工学系研究科数理情報学専攻数理情報第2研究室) [概要]

   組合せ最適化問題を線形計画で解く際にその制約式の本数は一般に膨大になる. その問題に対して, 新たな変数を導入することで問題を変えずに制約式を減らした拡張定式化を与えることができる例がある. また, 拡張定式化はYannakakis をはじめとする研究者らによりグラフの情報をやり取りする通信プロトコルを構成することで与えられることが示されている. 本発表ではネットワーク最適化問題の拡張定式化に対して, その通信プロトコルを構成する.

3. 対称行列の符号付けとグラフスペクトル / ○垣村 尚徳 (慶應義塾大学), Carlson Charles (University of Illinois, Urbana-Champaign), Chandrasekaran Karthekeyan (University of Illinois, Urbana-Champaign), Chang Hsien-Chih (University of Illinois, Urbana-Champaign), Kolla Alexandra (University of Illinois, Urbana-Champaign) [概要]

   対称行列の固有値はグラフ解析において重要な役割を果たしている．なかでも対称行列の非零要素に正負を割り当てて（符号付け）最大固有値を小さくする問題は，ラマヌジャングラフの存在証明の鍵となっている．本講演では，正則性や半正定値性など固有値に関する性質を満たすよう対称行列を符号付けする問題の計算複雑度を議論する．特に，対称行列の正則な符号付けを求める問題が多項式時間で計算できることを示す．

4. 一様半モジュラ束と付値マトロイド / ○平井 広志 (東京大学) [概要]

   マトロイドと幾何束の同等性(Birkhoff 1940)は，古くから知られている． この束によるマトロイドの特徴付けを付値マトロイド(Dress-Wenzel 1992)へと拡張する． 我々は，一様半モジュラ束という束を導入し，それが整数値付値マトロイドと同等であることを示す． これは，付値マトロイドに付随するトロピカル線形空間(Murota-Tamura 2001, Speyer 2008) の整数格子点のなす束の特徴付けにもなっており，付値マトロイドの完備化プロセス(Dress-Terhalle 1993)も含んでいる．

1. ２次元Delaunay図の逐次添加型３次元構成と入力順序によるパフォーマンス / ○岩本 龍馬 (和歌山大学大学院システム工学研究科), 今井 敏行 (和歌山大学システム工学部) [概要]

   メッシュの自動生成に有効である２次元Delaunay図の構成法として，初期三角形分割を構成し，フリップ操作で三角形分割を更新していくものがある．フリップは三角形分割のどこからどの順にでも行なえ，途中も三角形分割を維持できるなど利点が多い．本研究では，フリップを残しつつ，三角形分割構成を経由しない，３次元凸包を利用した構成法を示し，それが点の入力順序で実行時間のパフォーマンスがどのように変わるかを調べた．

2. 空間埋め込みの幾何情報を用いた骨格線計算 / ○森口 昌樹 (明治大学 先端数理科学インスティテュート) [概要]

   3次元形状の骨格線はコンピュータグラフィックスや形状処理において広く応用されている．応用によっては，表面メッシュへのマッピング（対応関係）を持った骨格線を構築することが必要である．さらに，マッピングはメッシュの埋め込み情報を保存することが重要である．本研究では，表面メッシュ内部の空間を分割せずに，埋め込み情報を保存した骨格線を計算する手法を提案する．

1. 抵抗率測定に使用される四探針法の数理モデルの構築と解析 / ○中野 泰河 (新潟大学理学部), 劉 雪峰 (新潟大学大学院自然科学研究科) [概要]

   四探針法は半導体材料の抵抗率を測定するために使用される方法である。材料内部の電位分布を計算するために、探針と材料の接触条件に関して幾つかの物理的な仮定が利用される。本研究では３つの仮定に応じて、微分方程式の境界値問題による数学的モデルを得た。さらに、探針と材料の接触面積が０に近づくとき、それぞれのモデルの解が同じ解に収束していること証明した。

2. アレルギー発症メカニズムの解析に向けた抗原・抗体の体内動態モデルの構築, 及び, Husbyらの実験データに対するパラメータ推定とその考察 / ○小松 瑞果 (神戸大学工学部情報知能工学科), 谷口 隆晴 (神戸大学システム情報学研究科/JST さきがけ) [概要]

   免疫とは，生体内に異物が侵入した際の自己防衛機能を指し，その働きが過剰であることをアレルギーという．異物, つまり, 抗原に対する抗体生産などを含む免疫応答によりある種の化学物質が生じ，アレルギー症状はこれによって引き起こされる．本研究では，体内における抗原・抗体の動態モデルを提案し，Husbyらによる実験データに対して適用する．また，データから推定されたパラメータの値などについて考察する．

1. 非有界線形作用素の作用素関数に対するShift-invert Rational Krylov法 / ○橋本 悠香 (慶應大学理工学研究科/理研AIP), 野寺 隆 (慶應大学理工学部) [概要]

   時間発展を含む偏微分方程式の数値解を求める手法には，行列関数とベクトルの積を用いる方法がある．本発表では，行列関数とベクトルの積を効率的に計算するKrylov部分空間法を提案する．対象となる行列は非有界な作用素を離散近似したものとなるため，値域が広範囲に分布するなど，非有界に近い振る舞いをする場合が多い．そこで，離散化を行う以前の非有界な線形作用素に関して考察することで，提案法の有効性を示す．

2. グラスマン多様体上のニュートン方程式の水平空間での表現とその求解について / ○佐藤 寛之 (京都大学), 相原 研輔 (東京都市大学) [概要]

   本発表では，グラスマン多様体をシュティーフェル多様体と直交群から構成される商多様体として扱い，その上の一般の目的関数の最適化問題，およびその解法のひとつであるニュートン法について議論する．特に，ニュートン法の各反復における探索方向が満たすべきニュートン方程式を水平空間上の線形方程式として導出し，さらにクリロフ部分空間法に基づいて，目的関数のヘシアンの表現行列を用いない反復解法を提案する．

3. 有限要素外積解析に対するRRGMRES法 / ○佐藤 智久 (神戸大学システム情報学研究科), 谷口 隆晴 (神戸大学システム情報学研究科，JSTさきがけ) [概要]

   抽象的Poisson問題に対する有限要素法である有限要素外積解析では，連立一次方程式の定式化のために，非正則な係数行列を作成した後，その係数行列の核に対応する，離散調和形式と呼ばれる関数の空間を求める必要がある．本発表ではrange restricted GMRES法（RRGMRES法）を用いることで，係数行列の核を求めることなく有限要素外積解析の理論解析が適用可能な解が得られることを示す．

4. 複数右辺ベクトルをもつ連立一次方程式に対するBlock BiCGGR法の近似解精度改善 / ○多田野 寛人 (筑波大学) [概要]

   複数右辺ベクトルをもつ連立一次方程式の反復法の一つであるBlock BiCGGR法は，漸化式で生成された残差と真の残差間のギャップが小さくなるように設計された方法である．しかしながら，同法ではこのギャップ発生の原因となる誤差項が存在しており，その影響を完全には打ち消せていない．本発表では，この誤差項の発生を抑える改良法を提案し，更なる近似解精度の改善を図る．

1. 単精度浮動小数点数環境にも有効な Augmented Implicitly Restarted Lanczos Bidiagonalization 法の改良 / 石田 遊也 (ヤフー株式会社), 高田 雅美 (奈良女子大学研究院生活環境科学系), ○木村 欣司 (京都大学大学院情報学研究科), 中村 佳正 (京都大学大学院情報学研究科) [概要]

   昨年度の研究部会連合発表会で発表したAIRLB法の改良は, 倍精度浮動小数点数環境では効果的であるが、単精度浮動小数点数環境では、そうではないことが判明した。そこで、単精度浮動小数点数環境にも有効な改良を改めて提案する。

2. 一般化固有値問題に基づく同時対角化の新しい応用：音源分離の高速化 / ○伊藤 信貴 (NTT), 荒木 章子 (NTT), 中谷 智広 (NTT) [概要]

   従来の音源分離技術では、高精度な音源分離が可能であるが、計算量が膨大で処理に長時間を要するため、応用範囲は大きく限定されていた。これに対し本発表では、一般化固有値問題に基づく同時対角化を応用することで、音源分離の精度を低下させることなく、上記の従来技術を大幅に高速化できることを示す。実験では、この高速化手法により、従来比250倍超の高速化が実現し、8秒の混合音に対する音源分離を、わずか2.7秒の処理時間で行うことができた。

3. 対称性を保存するblock SS–Hankel法について / ○今倉 暁 (筑波大学), 二村 保徳 (筑波大学), 櫻井 鉄也 (筑波大学、JST/CREST) [概要]

   指定領域内の固有値および対応する固有ベクトルを求める解法として，block SS–Hankel法が知られている．Block SS–Hankel法において，対象の固有値問題はblock Hankel行列を係数に持つ小規模な一般化固有値問題に帰着されるが，問題が対称一般化固有値問題である場合，帰着される固有値問題はその対称性が一般には保存されず，計算時間の増大および固有対の精度劣化を引き起こす．本講演では，対称性を保存するblock SS–Hankel法を提案し，数値実験からその有効性を検証する．

4. 少数のレゾルベントの線形結合の多項式をフィルタとする対称定値一般固有値問題の解法 / ○村上 弘 (首都大学東京) [概要]

   実対称定値一般固有値問題に対して，固有値が指定された区間に入る固有ベクトルは良く通過させるがそれ以外のものを強く除去する線形作用素をうまく構成してフィルタとする． それを用いると区間内の固有値に対応する不変部分空間を近似する空間の基底が構成できる． 少数（２～３個あるいは４個）のレゾルベントの線形結合の多項式を調整してフィルタに用いるが，構成の簡易さから多項式をチェビシェフ多項式に制限する場合を扱う．

1. Oakforest-PACSにおける一般化固有値計算の性能解析と性能予測 / ○星 健夫 (鳥取大学), 福本 智哉 (鳥取大学), 深谷 猛 (北海道大学), 山本 有作 (電気通信大学) [概要]

   超並列一般化固有値問題ミニアプリEigenKernel(星ら)に対して，Oakforest-PACSでの性能(消費時間)解析を行なった．さらに，性能モデリングとベイズ推定を組み合わせた，性能予測を試行した．上記は，大規模量子物質計算（電子状態計算）の基盤として，行なっている．特にノード数を増やしていく方向への外挿に大きなニーズがあり，最終的にはドライラン機能（実計算の前に消費時間を予測する機能）として，アプリに実装したい．

2. 特徴量スケーリングを用いたスペクトラルクラス分類 / ○松田 萌望 (筑波大学), 保國 惠一 (筑波大学), 櫻井 鉄也 (筑波大学、JST/CREST) [概要]

   スペクトラルクラスタリングは複雑なデータ分類において有効であるが、必ずしも所望の分類を与えるとは限らない。そこでデータの一部のラベル情報を用いたスペクトラルクラス分類手法を提案する。ラベル情報に基づいたFiedlerベクトルを用いて特徴量のスケールを調整するための因子を固有ベクトルとして持つ固有値問題を定式化する。これを解いて得られる因子をデータ全体に施すことで分類精度を向上させる。従来の教師付き分類手法と数値実験で比較して提案法の性能を評価する。

3. 多項式固有値問題のすべての固有値に対する数値的検証法 / ○相馬 彩乃 (岩手大学), 宮島 信也 (岩手大学) [概要]

   多項式固有値問題のすべての固有値に対する数値的検証法を提案する．このような方法は2010年にMiyajimaにより提案されている．この方法はすべての固有値に対して1つの誤差限界を与える．これに対して，本講演で提案する方法は各固有値に対してそれぞれ一般に異なる誤差限界を与える．さらに，提案する方法により得られた（複数の）誤差限界がMiyajimaの誤差限界に比べて同等以下であることを示す．提案する方法の計算コストはMiyajimaの方法の計算コストとほぼ同等である．

4. Verified numerical computation for the matrix principal logarithm / ○宮島 信也 (岩手大学) [概要]

   Two iterative algorithms are proposed for numerically computing an interval matrix containing the matrix principal logarithm. The first algorithm is based on a numerical spectral decomposition and requires only cubic complexity per iteration. The second algorithm is based on a numerical Jordan decomposition and applicable even for defective matrices.

1. 3次元高次テンソルくりこみ群におけるテンソルのリオーダリング手順の最適化 / ○山田 悠加 (筑波大学), 今倉 暁 (筑波大学), 今村 俊幸 (理研 AICS), 櫻井 鉄也 (筑波大学) [概要]

   近年，素粒子物理学において系の分配関数を求める手法として，テンソルネットワークを用いたアルゴリズムが注目されている． 本研究ではそのアルゴリズムの一つである高次テンソルくりこみ群(HOTRG)に着目する． HOTRGの計算コストの主要部は複数テンソルの縮約であり，一般に行列積に基づき実装される． この時テンソル要素のリオーダリングが頻繁に起こるという問題がある． 本発表では，分散並列実装を前提とし，リオーダリング時間の削減を目的としたリオーダリング手順の最適化手法を提案する．

2. SOR法の緩和パラメータの幾何学的解釈 / ○宮武 勇登 (名古屋大学), 曽我部 知広 (名古屋大学), 張 紹良 (名古屋大学) [概要]

   SOR（逐次過緩和）法は線形方程式に対する代表的な定常反復法である．本講演では，勾配系と呼ばれる常微分方程式系に対するある数値解法とSOR法の算法としての同値性を示すことで，SOR法の緩和パラメータに対して，ある変数変換のもとでステップサイズとしての意味付けを与える．さらに，その議論に基づき，緩和パラメータの適応的な設定方法などについて考察する．

3. 3次曲線の新たな行列式表示と2つの代数曲線の交点計算への応用 / ○菊地 充彦 (埼玉大学), 重原 孝臣 (埼玉大学) [概要]

   m次、n次の2つの平面代数曲線の交点を求める問題P(m,n)の数値解法として、問題を連立一般固有値問題に帰着する方法が知られている。この際、曲線を行列式表現する必要があり、Plestenjakの方法に従えばn次曲線はn(n+1)/2次の行列式で表現できるが、この方法では交点自体が求まらない場合や求まっても精度が著しく低下する場合が多い。本発表では、n=2,3の場合に対してn次曲線をn次の行列式で表現する方法を示し、これを用いるとP(m,n) (m,n=2,3)の数値解の精度が大幅に向上することを報告する。

1. 特異値分解による縮退を用いた形状最適化解析の高速化 　Acceleration of shape optimization analysis using degeneration by singular value decomposition / ○丹後 秀一 (名古屋大学), 畔上 秀幸 (名古屋大学) [概要]

   本報では、形状変更初期の結果を特異値分解することで得られる縮退ベクトルを 用いて、計算モデルを縮退することで、以降の計算では精度を保ちつつ、計算時 間を大幅に短縮することが可能であることを示す。

2. On the shape Hessian of a least-squares-type cost functional associated with a cavity identification problem / ○Rabago Julius Fergy (Nagoya University), Azegami Hideyuki (Nagoya University) [概要]

   This work examines a cavity identification problem through the framework of shape optimization. Particularly, the inverse problem of reconstructing the defect is studied by minimizing a least-squares-type cost functional. The first-order shape derivative or shape gradient of the cost functional is recalled and its second-order shape derivative or shape Hessian is computed using the approach of Sokolowski and Zolesio. Additionally, the shape Hessian at the solution of the PDE system describing the cavity identification problem is computed using a classical method.

3. Shape optimization realizing given vibration mode and its application to fish robot / ○Chancharoen Wares (Nagoya University), Azegami Hideyuki (Nagoya University) [概要]

   Recently, the importance of bio-inspired robots has been known as the innovate device for discovering in extremely dangerous area. The challenging area is making low energy consumption robot but still keeping a high performance. We focused on the fish swimming robot to make the preliminary design of robot. Many fish robot studies are focused on mimicking its structure with the real fish. However, fish-like robot design is controlling actuators to produce the maximum thrust against drag force of water. There is a well-known study about fish swimming by Lighthill, et at. Lighthill have found the equations of fish swimming by biological experiment. According to Lighthill’s study, we found that the optimize shape of fish-like robot approach to design the robot has the efficient energy consumption. Consequently, the fish robot should swim by its natural frequency mode in order as decrease its energy consumption. The dynamic stiffness matrix of linear elastic body and eigenfrequency of fish vibration have been considered as the state determination problem equation and the norm of error of our calculation comparing to biology experiment-based equation from Lighthill as objective cost function. Finally, numerical examples are analyzed by H1 gradient method can find optimized shape of fish-like robot.

4. 制約下，及び制約を緩めた質量内での，最小仕事量を有する質量分布 / ○海津 聰 (東京理科大学) [概要]

   　全質量に制約を有する場合の，最小仕事量を与える質量分布を求めたい． 　そのような目的の質量分布を，全質量の，制約を緩めた最小仕事量分布を与える質量分布で近似する方式を提案します．

1. 振動対流の同期現象とその最適化: 位相縮約によるアプローチ / ○河村 洋史 (海洋研究開発機構) [概要]

   振動的な熱対流状態にあるHele-Shawセルの同期現象を考える．振動対流の位相縮約法を定式化することにより，振動対流の相互同期および共通ノイズ同期を解析する．特に，これらの同期現象に対する最適化手法を開発する．

2. 数理・データ科学の融合による流体制御 / ○中澤 嵩 (大阪大学) [概要]

   PODを活用した流れ場の形状最適化問題を述べる．

3. 流体力規定を目的とした非定常粘性流れ場の形状設計 / 尾関 優汰 (岐阜工業高等専門学校 専攻科学生), ○片峯 英次 (岐阜工業高等専門学校) [概要]

   非定常粘性流れ場に置かれた孤立物体に対して，孤立物体に生じる抗力，揚力などの流体力を規定する形状設計問題の数値解析法を提案する．はじめに，形状最適化問題を定式化し，随伴変数法および物質導関数を利用して，領域変動の感度（形状勾配関数）を理論的に導出する．次に，導出された形状勾配関数に基づいて力法（あるいは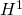勾配法）を適用し，Freefem++を利用して数値解析した簡単な二次元の解析例を紹介する．

1. ビットコインブロックチェーンの動作原理と安全性評価（仮） / ○佐古 和恵 (NEC) [概要]

   ビットコインで使われているブロックチェーンの動作原理を解説するとともに、検討中の安全性評価指標について紹介する。

2. ブロックチェーンと数理ファイナンス：サーベイ / ○関根 順 (大阪大学大学院基礎工学研究科) [概要]

   ブロックチェーン技術のもたらす革新が数理ファイナンス理論にどう反映されるか？その応用の可能性についてサーベイを行う。（数少ない）既存研究の紹介や、XVA解析の改善への試みを紹介したい。

1. Additional Default Probability from neighbor entities / ○KANEKO Takuya (ICU), HISAKADO Masato (Fintech Lab) [概要]

   In our presentation, we propose a methodology to effectively capture credit risk from neighbor entities. In short, our target is to numerically obtain additional credit risk from connected firms on network. Recently, commercial networks are available for investing and managing risk on professional information terminals like Bloomberg, Reuters, and Quick. They enable us to check commercial connection of firms. We utilize them to expect positive and negative effect on observing firms from neighbor firms especially when the neighbor firms have any credit events. We propose a methodology to analyze/measure impact which observing firms potentially receive from their neighbors. We applied Merton model which is generally utilized for credit risk management to calculate additional risk and simplified the formula for practicability/usability. Also, it enables us to escape from having any difficulties in computation time. We introduce our approach with over-viewing simple model guidance and explaining a few samples of numerical experiments.

2. 日本のクレジット市場における信用サイクルの変動要因 / ○廣中 純 (野村アセットマネジメント株式会社) [概要]

   本研究では, 市場で観測可能なファクター[信用イベントおよびマクロ経済要因]と市場で直接観測できないファクター(frailty)を考慮した信用イベント発生強度を表すモデルを提案する. また信用サイクルの変動要因を探るため, frailtyと信用サイクルを構成するファクターとの関連性について考察する.

3. 東証arrowheadリニューアル前後でのorder aggressivenessの分析 (Ⅱ) / ○佐藤 大地 (法政大学), 安田 和弘 (法政大学) [概要]

   本講演では9月24日に行われた東証arrowheadのリニューアルが与えた、投資家の注文執行に対する積極性の変化についての分析結果を報告する. 投資家の積極性はBiais et.al [1995]で提唱されたorder aggressivenessを用いることで、板情報からの取得が可能となる. また、昨年の2017年度年会で行った講演から更に対象銘柄を増やし、個別株単位での分析を行った.

4. 連続制御と確率インパルス制御の混合制御問題に対する数値計算アルゴリズムの提案 / 内藤 瞭介 (法政大学), ○安田 和弘 (法政大学) [概要]

   連続制御と確率インパルス制御の混合制御問題に対する数値計算アルゴリズムの一提案を行う．混合制御問題の例として，Cadenillas and Zapatero [2000]で考えられている中央銀行による金利操作を連続制御，為替介入を確率インパルス制御として持つコスト最小化問題が考えられる．このような問題に対し，Feng and Muthuraman [2010]が提案している確率インパルス制御問題への数値計算アルゴリズムを混合制御問題に拡張したアルゴリズムを提案する．

1. Computation of first-order Greeks for barrier options using chain rules for Wiener path integrals / ○石谷 謙介 (首都大学東京) [概要]

   In this presentation, we present a new methodology to compute first-order Greeks for barrier options under the framework of path-dependent payoff functions with European, Lookback, or Asian type and with time-dependent trigger levels. In particular, we develop chain rules for Wiener path integrals between two curves that arise in the computation of first-order Greeks for barrier options. We also illustrate the effectiveness of our method through numerical examples.

2. 損切りを考慮したペアトレード戦略に対する最適スイッチング / ○広瀬 翔 (東京工業大学大学院) [概要]

   相関の高い2つの金融商品が存在しているとき, それらのスプレッドが一定の水準に回帰していく性質を利用して収益を狙う投資戦略としてペアトレード戦略がある. これを実務に用いるためには, 損切りを考慮することが不可欠である. 本発表の目的は, 損切りを考慮した状態でポジションを構築・解消するための最適な閾値を確率制御アプローチにより導出することである.

3. Remarks on a copula-based conditional Value at Risk / ○石村 直之 (中央大学), Molina Barreto Andres Mauricio (Chuo University), 吉澤 容一 [概要]

   多変数Value at Riskについて，copulaとの関連でconditional Value at Risk(CCVaR)を考える．すなわち，Krzemienowski-Szymczykに従ってcopulaを用いてCCVaRを定義し，特にArchimedean copulaの場合に詳しい計算式を導く．

4. 受注データを用いた財務情報の推定と信用リスク評価 / ○山中 卓 (武蔵野大学) [概要]

   企業の受注データを利用して受注額変動モデルを構築し，モデルの信用リスク評価への応用を検討する．具体的には，受注額の変動から企業の将来財務を推定し，得られた推定財務情報から信用スコアリングを行う方法を示す．実企業の評価事例を示し，モデルの有用性を明らかにする．

1. Laplacianノルム評価を援用した楕円型線形作用素の可逆性検証 / ○渡部 善隆 (九州大学), 木下 武彦, 中尾 充宏 (早稲田大学) [概要]

   2階線形楕円型作用素に対する可逆性検証は，非線形問題の精度保証付き数値計算や固有値の除外範囲の特定のための重要な情報を与えます．本講演ではLaplacianのL2ノルムの上界を与えるための定式化の過程で導かれる可逆性条件が既存の手法の可逆性条件より良い結果を与えることを具体的な検証例を用いて示します．

2. Proudman-Johnson方程式のunimodalな解に対する計算機援用証明 / ○宮路 智行 (明治大学), 岡本 久 (学習院大学) [概要]

   2次元Navier-Stokes流れのある種の自己相似解を表すProudman-Johnson方程式に対するunimodalな定常解の存在を精度保証付き数値計算によって証明する．本研究における計算機援用証明のための基本的なアイデアは，定常問題を一階の常微分方程式系に変形して射撃法の定式化を行い，区間Newton法を適用することである．ただし，高Reynolds数流れにおいては射撃法の数値的不安定性が非常に厳しくなる．我々は多段射撃法と多倍長浮動小数点数演算を適用してこの困難を解決する．

3. 二次形式を用いたaffine arithmeticの拡張について / ○中山 大輔 (電気通信大学), 松田 望 (電気通信大学), 山本 野人 (電気通信大学) [概要]

   区間演算の一種であるaffine arithmeticは非線形な演算を一次式で近似するため、割り算などに対して精度が出にくい場合がある。本講演では、二次形式を用いてaffine arithmeticを拡張すると非線形演算がどの程度改善されるかを数値例を用いて示す。

4. 片側急減衰関数の無限積分に対するSE公式の改善と理論誤差評価 / ○鶴田 早紀 (広島市立大学), 花田 脩 (広島市立大学), 岡山 友昭 (広島市立大学) [概要]

   被積分関数が解析的かつ遠方で急速に0に近づく（急減衰関数の）とき，無限積分に対する複合台形則は非常に高精度であることが知られている． しかし，∞方向には急減衰だが，－∞方向には急減衰でない場合も考えられる． この場合には，変数変換により被積分関数を急減衰関数に変形する方法がStengerによって提案されている．ただしこの変数変換には改善の余地があり，本研究では新たに2通りの変数変換を提案する．さらに，それぞれについて誤差の見積もりが可能な誤差評価を行った．

1. 半線形楕円型境界値問題の高エネルギー解に対する精度保証付き数値計算 / ○酒井 将大 (早稲田大学), 田中 一成 (早稲田大学), 大石 進一 (早稲田大学) [概要]

   半線形楕円型境界値問題の高エネルギー解に対する精度保証付き数値計算をNewton-Kantorovichの定理に基づき行った結果を報告する。通常逆作用素ノルムと残差ノルムの積で評価するNewton法の修正項のノルムを、線形化問題の精度保証を介して上下からより厳密に評価する。本手法が特に起伏の激しい高エネルギー解の精度保証に有効であることを報告する。また同じ近似解に対してその誤差上限の評価が100倍以上改善される例を紹介する。

2. 優解劣解法を用いたアレンカーン方程式の解の精度保証付き数値計算 / ○松嶋 佑汰 (早稲田大学), 田中 一成 (早稲田大学), 大石 進一 (早稲田大学) [概要]

   優解劣解法を用いてアレン・カーン方程式の初期値問題に対する精度保証付き数値計算を行った結果を報告する。本手法は同問題の正値解を対象とし、元の方程式に僅かな摂動を与えることで各時間区間毎の優解劣解を数値的に構成した後にその間に真の解が時間局所的に存在することを示す。 結果として、構成した優解劣解の上下関係を精度保証付きで確認するだけで、解の存在性をその定量的な評価と共に検証可能であることを報告する。

3. Affine Arithmeticを用いた遅延微分方程式の解の精度保証 / ○青木 柊 (早稲田大学), 柏木 雅英 (早稲田大学) [概要]

   遅延微分方程式の精度保証付き数値解法は既に提案されているが、長い範囲にわたって計算する際の区間幅の増大が問題となっていた。そこで、本講演ではAffine Arithmeticを用いて遅延微分方程式の解をより高精度に計算する方法を提案する。まずべき級数の係数をAffine型に変更した新手法を提示し、次に数値例によりその有効性を示す。

1. 三乗和と五乗和に関するディオファントス方程式の自然数解の探索 / ○五百旗頭 学 (大阪大学理学研究科数学専攻博士前期課程2年) [概要]

   三乗和と五乗和に関する、あるディオファントス方程式の非自明な自然数解を、有理数体上の楕円曲線の理論を用いて探索した。同方程式の非自明な整数解を探索する方法が先行研究として知られていたが，今回はそれを詳しく分析して、非自明な自然数解を探索する方法に改良した。また、この方法によって非自明な自然数解を無数に計算できることを証明した。

2. 楕円曲線Hidden Number Problem のEdwards 曲線への拡張 / ○小野澤 綜大 (東京大学), 高安 敦 (東京大学/産業技術総合研究所), 國廣 昇 (東京大学) [概要]

   Hidden Number Problem (HNP)はDiffie-Hellman鍵共有における共有鍵の上位ビットが漏洩した時の安全性を評価する目的で，Boneh とVenkatesan (CRYPTO'96) が導入した問題である．楕円曲線Diffie-Hellman (ECDH)鍵共有におけるHNP は楕円曲線の演算が複雑なため長く行われてこなかったが，Shani (PKC2017) は式変形を工夫することで解析を行った．Shani の研究では ECDH鍵共有で一般的に用いられる Weierstrass 標準形について解析を行っている． 本研究では近年，暗号方式へ応用されつつあり注目されているEdwards 標準形における HNP を多項式時間で解くアルゴリズムを提案する．まず，我々は Edwards 曲線の加算公式と標準形の定義式を元に共有鍵の未知部分が解となる法付き方程式を導出する．そして，その方程式を Coppersmith の手法を用いることで解く．我々の手法では上位ビットの約83%が得られた時に共有鍵を復元できる．

3. 低次元におけるLLL簡約基底が最短ベクトルを含まない必要十分条件 / ○松田 康太郎 (東京大学), 高安 敦 (東京大学), 高木 剛 (東京大学) [概要]

   最短ベクトル問題(SVP)の近似解を求める多項式時間アルゴリズム としてLLLアルゴリズムがある. 本研究では, 3,4次元の場合, LLLアルゴリズムの出力から 最短ベクトルを求める厳密解法を考察する. まず, Lovasz条件のパラメータδが1に近い場合, 3,4次元の LLL簡約基底が非零最短ベクトルを含まない必要十分条件を求める. これによって, LLL簡約基底の{-1,0,1}のみを係数とする線型結合の 一部を調べることで, 非零最短ベクトルが得られることを示す.

4. HFERP – A New Multivariate Encryption Scheme / ○池松 泰彦 (九州大学), Perlner Ray (NIST), Smith-Tone Daniel (NIST, University of Louisville), 高木 剛 (九州大学), Vates Jeremy (University of Louisville) [概要]

   多変数多項式暗号は量子計算機に耐性を持つ公開鍵暗号の候補の一つである。 2016年安田氏らによりSRPという多変数多項式暗号が提案された。これはSquare,Rainbowという二つの暗号、署名方式を、Squareで用いられる変数がRainbowのVinegar変数になるように組み合わせ、さらにランダムな二次多項式を付加(Plus)して、SquareとRainbowの構造を隠すことで構成される。しかし、2017年Perlner氏らはMinRank攻撃の計算量がグレブナー基底のものより下回ることを証明し、MinRank攻撃が有効であることを示した。これは、Squareの公開鍵から得られる行列たちの最低ランクが1であるということから従う。 この講演では、Squareの部分を多変数多項式暗号HFEに代替したHFERPという新しい暗号方式を提案する。さらに、HFEの公開鍵から得られる行列たちの最低ランクがSquareの場合よりも高くなることを述べ、結果的にHFERPへのMinRank攻撃が有効に働かなくなることを説明する。最後にHFERPの80bit securityに対するパラメータを提案する。

1. GVWアルゴリズムの改良とその実験的評価 / 馬渕 圭史 (九州大学大学院数理学府), ○池松 泰彦 (九州大学マス・フォア・インダストリ研究所) [概要]

   グレブナー基底導出アルゴリズムの1つとして，2010 年に S. Gao, F. Volny IV, M. Wang らによって提案されたGVWアルゴリズムがある．GVWアルゴリズムでは多くの “reduction” を実行するが，従来の高速化手法を拡張することでreduction 数を削減できる．本講演では，高速化手法の拡張を適用したアルゴリズムを数式処理ソフトMagmaで実装し，オリジナルのGVWアルゴリズムと比較評価することで見られる改良手法の効果を説明する．

2. BLS 曲線における Optimal Ate Pairing の実装と評価 / 馬渕 圭史 (九州大学), ○横山 俊一 (九州大学), 齋藤 恆和 (NTTセキュアプラットフォーム研究所) [概要]

   次世代の公開鍵暗号方式として、任意の ID を公開鍵として利用できる ID ベース暗号があり、実際のサービスへの利用が進んでいる。この ID ベース暗号の多くは楕円曲線上のペアリングを用いて実装されており、安全性はそのペアリングについての離散対数問題の困難性が仮定となる。 CRYPTO2016 において Kim 等は任意のペアリングについての離散対数問題に対する解析手法の改良を提案し、ペアリングの安全性レベルが下がった。この解析手法に耐えうるものとして、SCIS2017 において清村等は 256 ビット安全なペアリングのパラメタとして BLS48 のパラメタを提案した。 本講演では、ID ベース署名の OSS である libsnark を元に BLS48 のパラメタを用いて Optimal Ate Pairing (OAP) を実装し、さらに libsnark 内のペアリングパラメタ BN256 との OAP と比較評価する。

3. 平面4次曲線の線形行列式表示を計算するアルゴリズムについて / 石塚 裕大 (京都大学理学研究科), 伊藤 哲史 (京都大学理学研究科), ○大下 達也 (愛媛大学理工学研究科) [概要]

   平面曲線の定義方程式を，線形形式成分の正方行列の行列式で 表すことを「線形行列式表示」という．線形行列式表示の計算は， 19世紀のHesseの研究に遡る伝統的な問題であり，Jacobi多様体 のMordell-Weil群を計算する問題や，直線束の極小分解を計算 する問題と関係することが分かっている．最近では，この問題は， 数論的不変式論の観点からも注目されるようになってきた． この講演では，Klein 4次曲線などの具体的な平面4次曲線について， その線形行列式表示を計算するアルゴリズムの解説を行う． また，具体的な計算結果の紹介を行う．

4. 多重ゼータ値の行列のランク計算へSATのアルゴリズムを応用する研究 / ○町出 智也 (国立情報学研究所（JST ERATO 河原林巨大グラフプロジェクト）), 薗部 知大 (国立情報学研究所（JST ERATO 河原林巨大グラフプロジェクト）) [概要]

   　多重ゼータ値は Riemann ゼータ関数の特殊値の一般化です。昨今、金子-野呂-鶴巻氏等は、ガウスの消去法を用いて、多重ゼータ値のある線形関係式の集合に対応する行列のランクの上限を計算しました。本講演では、SAT に使用されるアルゴリズムを応用した、ランク計算のアルゴリズムを紹介します。そして、速度などのある点においてはガウスの消去法と同等かそれ以上の性能になることの実験結果を報告します。

1. 円分体の相対類数の行列式公式の値の大きさの特異性について / ○谷口 哲也 (金沢工業大学 基礎教育部) [概要]

   円分体の相対類数の行列式公式としてDemjanenko 行列，Maillet行列など多数知られているが，これらの行列式の値は係数をランダムに生成して配置した行列式に比べ「極端に大きい」ことを，講演者は数値的に観察している．例えばp=101 円分体では，相対類数公式の行列式値は，平均から4.7標準偏差ほど大きな位置にあり，またHadamard行列がまだ見つかっていない716次行列に対応するDemjanenko行列式の値も極めて大きく，Hadamardの上限の約96.8%の大きさの桁数を実現している． この「行列式の値が大きい」という現象は，たとえば実験計画法などの実学的な応用につながると講演者は考えている（実験計画法では実験効率を上げるために，±1 成分の行列で行列式値が大きなものが利用される）． 本講演ではこれまでに行った数値実験結果，とくに行列式の値の分布，固有値の分布，±1成分のDemjanenko行列から得られる球面上の点の配置に関する数値実験結果および，「ランダムに係数を生成した行列」「Demjanenko行列」「Hadamard行列」を，距離行列と対応付けて比較した結果について報告する．時間が許せば他の行列での相対類数公式でも同様の現象が起こっていることも報告したい．

1. 画像の平行移動量と回転角度の検出について / ○守本 晃 (大阪教育大学), 芦野 隆一 (大阪教育大学), 萬代 武史 (大阪電気通信大学) [概要]

   元画像に対して，平行移動と回転の入った画像の重み付き重ね合わせを観測し， 複数の観測画像から元画像の分離問題を考えよう． 本講演では，２枚の観測画像から元画像の相対平行移動量と相対的回転角度を推定するために， フーリエ空間でモジュレーションを行った後， ドーナッツ領域を取り出し，極座標表示を行い巡回畳み込みを用いて， 平行移動量と回転角度を求める方法を述べる．

2. ウェーブレットの逆変換公式について / ○竹本 奈央 (奈良女子大学大学院人間文化研究科) [概要]

   古典的な連続ウェーブレットの逆変換公式は, アドミッシビリティ・コンディションを満たすときのみ与えられていた. しかし, 2014 年に Lebedeva とPostnikov により, その条件を満たさない場合でも有効である, 新たな1次元の逆変換公式が与えられた. 本講演では, 森藤紳哉との共同研究について述べる. 具体的には, 彼らの公式の多次元版とクリフォード代数の設定にまで拡張した結果, 及びストックウェル変換に関する逆変換公式についてである.

1. 聴性誘発脳波解析とウェーブレット関数について / ○井川 信子 (流通経済大学), 守本 晃 (大阪教育大学), 芦野 隆一 (大阪教育大学) [概要]

   聴性誘発脳波解析にウェーブレット関数を用いる際，これまでは， 聴性誘発脳波解析において必要な情報が得られることを主体的に考えてきた． 本発表では，必要な情報が得られることを前提にしつつ，ウェーブレット解析の 観点から，ウェーブレット関数の的確な適用等についての議論を試みたい．

2. 4次のStrömbergウェーブレットの構成について / ○福田 尚広 (松江工業高等専門学校), 木下 保 (筑波大学) [概要]

   本講演では，これまでのStömberg ウェーブレットの導出方法を再考し，新たな類似タイプのスプラインウェーブレットを導く．また，一般的に利用されるスプライン関数に対応する4 次のStömberg ウェーブレットと，その類似タイプに関する，対称性などの性質について報告する．

1. Constructive a priori error estimates for Galerkin-Wavelet solution of two-point boundary value problems / ○Ali Amjid (Saga university), Omura Hajime (Saga university), Minamoto Teruya (Saga university) [概要]

   Constructive error estimates play a significant role in the numerical verification methods of solutions for nonlinear partial differential equations. There are several a priori error estimates for finite element approximate solutions of elliptic partial differential equations. We consider the constructive a priori error estimates for a Galerkin-Wavelet approximation of the two-point boundary value problems. We use the Daubechies wavelets of order two which are compactly supported and form an orthonormal basis of the space of square integrable functions. We show some numerical examples demonstrating the effectiveness of our error estimates. These estimates will be very useful in the development of the numerical verification method for solutions of elliptic partial differential equations.

2. リフティング複素ウェーブレットによるコンパクトな深層学習モデルの実現 / ○高野 茂 (九州大学) [概要]

   リフティング複素ウェーブレットに基づくコンパクトな新しい深層学習モデル（LcwtNet）を提案する。提案するLcwtNetは、既存の深層学習モデルであるCNNをベースに、特徴抽出層をリフティング複素ウェーブレット変換に置き換える。実験では、画像識別の精度を落とさずに深層学習モデルのパラメータ数を削減できることを示す。

1. ランチョス・フィリップスアルゴリズムの可積分性とその直交多項式への応用 / ○澤 薫 (京都大学工学部), 中村 佳正 (京都大学情報学研究科) [概要]

   ランチョス・フィリップスアルゴリズムはランチョス法から導出されるハンケル行列のコレスキー分解を計算するアルゴリズムである. その計算過程で, 直交多項式の三項間漸化式の係数が計算される. 一方, qdアルゴリズム（離散戸田格子）もまたランチョス法から導出でき, 直交多項式の三項間漸化式の係数を計算することができる. 本発表では, 2つのアルゴリズムを比較し, さらに, ランチョス・フィリップスアルゴリズムの可積分性について考察する.

2. I型離散ハングリー戸田方程式を用いた固有値および要素を指定した上ヘッセンベルグ行列の構成法 / ○赤岩 香苗 (京都産業大学), 谷口 雄大 (同志社大学), 近藤 弘一 (同志社大学) [概要]

   逆固有値問題の1つに、指定した固有値をもつ行列を構成する問題がある。発表者らはこれまで、I型離散ハングリー戸田方程式を用いた上ヘッセンベルグ行列の逆固有値問題の解法を提案している。本講演では、固有値だけでなく行列の一部の要素を指定する場合であっても、I型離散ハングリー戸田方程式を用いて上ヘッセンベルグ行列が構成できることを示す。

3. ヘッセンベルグ行列が現れるラックス可積分系について / ○新庄 雅斗 (京都大学), 岩崎 雅史 (京都府立大学), 近藤 弘一 (同志社大学) [概要]

   ラックス形式は力学系の可積分性に起因する性質の1つといえる．有名な戸田方程式は3重対角行列を用いたラックス形式で表現され，離散された戸田方程式はそのラックス形式が3重対角行列のLR変換を与える漸化式と見なせる．本講演ではヘッセンベルグ行列のLR変換およびその連続極限を考察することで，ラックス形式がヘッセンベルグ行列に係わる連続と離散の可積分系を明らかにする．

4. トロピカル3重対角行列の固有値を計算する超離散ロトカ・ボルテラ系 / ○福田 亜希子 (芝浦工業大学), 渡邉 扇之介 (小山工業高等専門学校), 花岡 歩 (京都府立大学), 岩崎 雅史 (京都府立大学) [概要]

   線形代数における対称3重対角行列の固有値を求めるための数値解法として，可積分な離散ロトカ・ボルテラ系に基づくdLVアルゴリズムが知られている。dLVアルゴリズムの核となる漸化式は離散ロトカ・ボルテラ系である。 本講演では，離散ロトカ・ボルテラ系を超離散化（トロピカル化）した超離散ロトカ・ボルテラ系を利用すると，Min-Plus代数における対称な3重対角行列の固有値が求まることを示す。

1. 棒のたわみ問題のグリーン関数とソボレフ不等式の最良定数 / ○山岸 弘幸 (都立高専) [概要]

   弾性基盤で支えられた棒の両端に張力をかけ、外力を加えた時のたわみは、４階線形常微分方程式の境界値問題で記述される。境界条件は周期、両端ディリクレ、両端ノイマン、片側ディリクレ片側ノイマンの４種の条件を考える。境界値問題の解の積分核であるグリーン関数を具体的に求めた。境界値問題から派生するヒルベルト空間で、グリーン関数は再生核としての性質をもつ。再生等式にシュワルツ不等式を適用するとソボレフ不等式が導出できる。ソボレフ不等式はたわみの最大幅を、たわみのポテンシャルエネルギーの定数倍で評価する不等式であり、定数のうち最も小さい定数である最良定数を求めた。最良定数はグリーン関数の対角成分の最大値であり、弾性基盤のバネ定数と張力で記述できる。さらに、ソボレフ不等式で定数を最良定数に置き換えたときの等号を達成する関数もグリーン関数のある断面で記述できる。棒のたわみの最大幅とその形状を関数で表すことができる。

2. ロジスティックデータへのゴンペルツモデル適用で得られた飽和推定値の凸性 / ○佐藤 大輔 (NTT) [概要]

   ロジスティックモデルとゴンペルツモデルは予測に使われる代表的なモデルである．しかし初期段階で実データがどちらのモデルに相応しいのかの判定方法がない．あえて異なるモデルを適用したときに飽和値がどのように変化するのかの厳密な解析はその判定に大きな指針を与えるため重要である．本論では厳密解を持つ差分方程式を用いた厳密解析を行い推定飽和値がデータ数に対して下に凸であることを示す．

3. 土壌中の水浸透現象に対する可積分離散モデルの比較検討 / Triadis Dimetre (九大IMI), ○梶原 健司 (九大IMI), Broadbridge Philip (ラ・トローブ大), 丸野 健一 (早稲田大) [概要]

   土壌の水浸透を記述するBroadbridge-Whiteモデルの可積分離散化を考察する．モデル方程式がホドグラフ変換でBurgers方程式に帰着することに注目し，離散モデルを線形拡散方程式をベースに自己適合移動型格子スキームとして定式化する．線形レベルでを数値精度を考慮してCrank-Nicholsonスキームを採用した結果と，同スキームをモデル方程式に直接適用して計算した結果を比較し，可積分離散モデルの有効性を示す．

4. 離散対数型美的曲線の離散変分原理による定式化 / ○梶原 健司 (九大IMI), Schief Wolfgang (ニューサウスウェールズ大), 朴 炯基 (九大数理) [概要]

   対数型美的曲線に対する相似幾何による定式化に基づき，可積分離散化の手法を適用して離散対数型美的曲線を構成する．また，離散フェアリングエネルギーを導入して離散対数型美的曲線をその臨界点として特徴付ける．

1. DAHA代数と単位円周上の直交多項式 / ○辻本 諭 (京都大学大学院情報学研究科), Vinet Luc (Centre de recherches mathematiques Universite de Montreal), Zhedanov Alexei (School of Information, Renmin University of China) [概要]

   DAHA(double affine Hecke algebra)の三重対角の生成元による無限次元表現について議論する．さらに，この表現から単位円周上の直交多項式(OPUC)を導き，Askey-Wilson多項式のOPUC類似について考察する．

2. -1-Jacobi多項式の例外型拡張について / ○羅 宇 (京都大学), 辻本 諭 (京都大学) [概要]

   近年、古典直交多項式のq-Askey Schemeの頂点に立つq-Racah多項式の(非自明な)-1極限であるBannai-Ito多項式が、Dunkl型差分作用素の固有関数と確認され、新たに古典直交多項式として認識された。それから、Bannai-Ito多項式の下にあるBig -1 Jacobi多項式とLittle -1 Jacobi多項式もDunkl型微分作用素の固有関数として発見された。本講演ではこれらの-1 Jacobi多項式に対して、例外型拡張を構成する。さらに、我々が以前に紹介した例外型Bannai-Ito多項式との関係についても考察を加えていく。

3. DKP方程式のソリトン解のロンスキ型パフィアン表示に関するネットワークを用いた解析 / ○城戸 真弥 (早稲田大学基幹理工学部応用数理学科), 田中 悠太 (早稲田大学基幹理工学研究科数学応用数理専攻), 渡邉 靖之 (早稲田大学基幹理工学研究科数学応用数理専攻), 丸野 健一 (早稲田大学理工学術院), 筧 三郎 (立教大学理学部) [概要]

   KP方程式のソリトン解のロンスキアン表示は完全置換やネットワークと関係し，それらを用いてKP方程式のソリトン相互作用の詳細な研究がなされている．KP方程式の一般化として得られる方程式の一つであるDKP方程式のソリトン解のロンスキ型パフィアン表示について同様な解析を行うことを目指し，ロンスキ型パフィアン表示とネットワークの関係を整備する．

4. exponential Newell-Whitham モデルの超離散化とその解 / ○鈴木 大庸 (法政大学大学院), 礒島 伸 (法政大学) [概要]

   以前, 交通流モデルの 1 つであるexponential Newell-Whitham(eNW) モデルの, 時間離散化を行った.　また, 従属変数を1個もしくは2個持つ双線形形式をそれぞれ導き，その特殊解を構成し,比較を行った．本発表ではeNWモデルの超離散化を行い, 特殊解を求めるとともに, 離散時間eNWモデルとの比較を行う.

1. 超離散2次元戸田方程式のソリトン解 / ○長井 秀友 (東海大学理学部) [概要]

   本発表では超離散2次元戸田方程式の超離散パーマネント解、およびその証明方法を紹介する。 具体的には、先行研究で知られているヤコビの恒等式の超離散対応物に対して、ある条件を付け加えることで、離散系と同様の手順で超離散2次元戸田方程式の解を導くことができることを示す。 さらに、得られた解が離散2次元戸田方程式のソリトン解の超離散化によっても得られることを紹介する。

2. フィルター型セルオートマトンの解の構造 / ○石井 裕子 (早稲田大学大学院基幹理工学研究科), 西山 慎一郎 (早稲田大学基幹理工学部), 高橋 大輔 (早稲田大学大学院基幹理工学研究科) [概要]

   フィルター型セルオートマトン(FCA)とは、前の時刻の大域的な情報から定まるという特別な依存性を持ったセルオートマトンである。本研究では、ブール演算で定義 された時間1階2近傍FCAをmin方程式に拡張し、半無限領域での初期値境界値問題を解き、解の漸近挙動を調べた。講演ではこれらの結果について述べる予定である。

3. 確率過程的手法を用いた確率セルオートマトンの解析 / ○延東 和茂 (早稲田大学) [概要]

   確率セルオートマトンの漸近挙動を解析する際、基本図と呼ばれる運動量平均の保存量密度依存性を理論的に導出するため、分解予想という手法を用いることがある。分解予想はその存在が数値的検証によって確かめられているのみであるが、本講演では、確率過程と組み合わせ論における基本的な手法を用いて、分解予想の存在についての考察を行う。また、分解予想を用いずに基本図を導出する手法についても議論する。

4. 大域的2次元セルオートマトンのある拡張について / ○由良 文孝 (公立はこだて未来大学) [概要]

   中村・岩尾・高橋(2007)によって提案された、大域的情報に基く時間発展ルールを持つ二次元セルオートマトン(GCA)は、通常のCAとは異なり、2次元面内の閉曲線の形状に基づくルールを持つ．本講演ではGCAの多状態への拡張を定義し、その新奇な振る舞いやGCAによる計算モデルの可能性を紹介する．